Python计算圆周率

第一次python上机课，老师找了一个知乎上的问题：“ 圆周率pi比较著名的无穷级数公式有哪些？”
好家伙，原来前人研究了这么多使用级数计算圆周率的方法，五种方案的详细叙述在
https://www.zhihu.com/question/402311979

方案一：

%matplotlib inline
import matplotlib.pyplot as plt
import math
# matplotlib 中文支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号


# 根据求解方案一，计算结果和收敛过程
temp = 0
n = 0
x_list = []
y_list = []

while n<628:
    temp += (-1)**n/(2*n+1)
    Pi = 4 * temp    
    y_list.append(Pi)
    x_list.append(n)
    n +=1
    
print("n从0开始取，项数N=628, value of Pi is {}（四舍五入）".format(round(Pi,2)))
print('Exact value is: ',Pi)

plt.plot(x_list, y_list)
plt.title('方案一计算收敛图')
plt.xlabel('N value')# x轴标题
plt.ylabel('Pi value')  # y轴标题
plt.show()

n从0开始取，项数N=628, value of Pi is 3.14（四舍五入）
Exact value is:  3.1400002979112887

方案二：

# 根据求解方案二，计算结果和收敛过程,由于收敛极快，不便于可视化展示，我们打印输出观察收敛情况。

def doubleFactorial(n):
    ans=1                         #初始值
    for i in range(n,0,-2):    #循环遍历
        ans*=i                    #2021*2019*2017*····*3*1
    return ans

def solve2(N):
    temp2 = 0
    n_2 = 0
    while n_2<N:
        temp2 += doubleFactorial(2*n_2+1)/(doubleFactorial(2*n_2)*(2*n_2+1)*(2*n_2+1)*math.pow(2,2*n_2+1))
        n_2 += 1
    Pi_2 = 6*temp2
    return Pi_2

print("n从0开始取，项数N=3, value of Pi is {}（四舍五入后）".format(round(solve2(3),2)))

for i in range(10):
    print('N={0}, the exact value of Pi is {1}'.format(i,solve2(i)))

n从0开始取，项数N=3, value of Pi is 3.14（四舍五入后）
N=0, the exact value of Pi is 0
N=1, the exact value of Pi is 3.0
N=2, the exact value of Pi is 3.125
N=3, the exact value of Pi is 3.1390625
N=4, the exact value of Pi is 3.1411551339285717
N=5, the exact value of Pi is 3.14151117234003
N=6, the exact value of Pi is 3.141576715774867
N=7, the exact value of Pi is 3.141589425319122
N=8, the exact value of Pi is 3.141591982358383
N=9, the exact value of Pi is 3.141592511157863

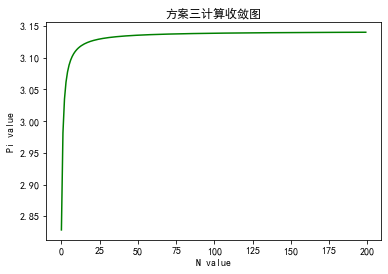
方案三：

# 根据求解方案三，计算结果和收敛过程

temp3 = 0
n_3 = 0
x_list3 = []
y_list3 = []
while n_3 < 200:
    temp3 += 1/(2*n_3+1)**2
    Pi_3 = math.sqrt(8 * temp3)
    y_list3.append(Pi_3)
    x_list3.append(n_3)
    n_3 += 1
    
print("n从0开始取，项数N=200, value of Pi is {}（四舍五入）".format(round(Pi_3,2)))
print('Exact value is: ',Pi_3)

plt.plot(x_list3, y_list3, 'g')
plt.title('方案三计算收敛图')
plt.xlabel('N value')# x轴标题
plt.ylabel('Pi value')  # y轴标题
plt.show()

n从0开始取，项数N=200, value of Pi is 3.14（四舍五入）
Exact value is:  3.140000704127709

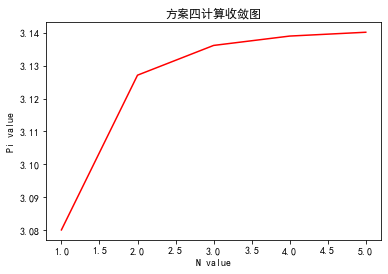
方案四:

# 根据求解方案四，计算结果和收敛过程

temp4 = 0
n_4 = 1
x_list4 = []
y_list4 = []
while n_4<6:
    temp4 += 1/n_4**4
    Pi_4 = math.pow(90*temp4, 1/4)
    y_list4.append(Pi_4)
    x_list4.append(n_4)
    n_4 += 1

print("n从1开始取，项数N=5, value of Pi is {}（四舍五入）".format(round(Pi_4,2)))
print('Exact value is: ',Pi_4)

plt.plot(x_list4, y_list4, 'r')
plt.title('方案四计算收敛图')
plt.xlabel('N value')# x轴标题
plt.ylabel('Pi value')  # y轴标题
plt.show()

n从1开始取，项数N=5, value of Pi is 3.14（四舍五入）
Exact value is:  3.140161179474259

方案五：

'''根据求解方案五，计算结果和收敛过程，由于只需极小的N即可达到收敛，
无需进行可视化，定义计算 Pi 的函数，计算前几个N值观察即可。'''

def PiCalcute5(N):
    n_5 = 0
    temp5 = 0
    while n_5 <= N:
        temp5 += (math.factorial(4*n_5)*(26390*n_5+1103))/(math.pow(math.factorial(n_5),4)*math.pow(396,(4*n_5)))
        n_5 += 1
    Pi_5 = 9801/(temp5*(2*math.sqrt(2)))
    return Pi_5

print("While N=1,the estimate value of Pi is {0:.2f}（四舍五入）".format(round(PiCalcute5(1),2)))
print('n=1, Pi=',PiCalcute5(1))
print('n=2, Pi=',PiCalcute5(2))
print('n=3, Pi=',PiCalcute5(3))
print('n=4, Pi= ...')

While N=1,the estimate value of Pi is 3.14（四舍五入）
n=1, Pi= 3.141592653589794
n=2, Pi= 3.141592653589793
n=3, Pi= 3.141592653589793
n=4, Pi= ...

求解方案的效率对比：

我们还可以计算对比五种求解方案的效率，借助datetime库计算不同计算方案下， 达到指定精确度（3.14）时所用的时间

import pandas as pd
from timeit import default_timer as timer

'''为了对比五种级数计算算法的效率，我们可以借助datetime库计算不同计算方案下，
达到指定精确度（3.14）时所用的时间'''

# 方案一：
start1 = timer()

temp1 = 0
n1 = 0
while n1 < 628:
    temp1 += (-1) ** n1 / (2 * n1 + 1)
    n1 += 1
Pi_1 = 4 * temp1

end1 = timer()
t1 = (end1 - start1) * 1000
print('方案一： ', Pi_1)
print('Running time: %s ms' % t1)

# 方案二：
start2 = timer()

def doubleFactorial(n):
    ans = 1  # 初始值
    for i in range(n, 0, -2):  # 循环遍历
        ans *= i  # 2021*2019*2017*····*3*1
    return ans

temp2 = 0
n_2 = 0
while n_2 < 3:
    temp2 += doubleFactorial(2 * n_2 + 1) / (
            doubleFactorial(2 * n_2) * (2 * n_2 + 1) * (2 * n_2 + 1) * math.pow(2, 2 * n_2 + 1))
    n_2 += 1
Pi_2 = 6 * temp2

end2 = timer()
t2 = (end2 - start2) * 1000
print('方案二： ', Pi_2)
print('Running time: %s ms' % t2)

# 方案三：
start3 = timer()
temp3 = 0
n_3 = 0

while n_3 < 200:
    temp3 += 1 / (2 * n_3 + 1) ** 2
    n_3 += 1
Pi_3 = math.sqrt(8 * temp3)

end3 = timer()
t3 = (end3 - start3) * 1000
print('方案三： ', Pi_3)
print('Running time: %s ms' % t3)

# 方案四：
start4 = timer()
temp4 = 0
n_4 = 1

while n_4 < 6:
    temp4 += 1 / n_4 ** 4
    n_4 += 1

Pi_4 = math.pow(90 * temp4, 1 / 4)
end4 = timer()
t4 = (end4 - start4) * 1000
print('方案四： ', Pi_4)
print('Running time: %s ms' % t4)

# 方案五：
start5 = timer()
n_5 = 0
temp5 = 0
while n_5 <= 1:
    temp5 += (math.factorial(4 * n_5) * (26390 * n_5 + 1103)) / (
                math.pow(math.factorial(n_5), 4) * math.pow(396, (4 * n_5)))
    n_5 += 1
Pi_5 = 9801 / (temp5 * (2 * math.sqrt(2)))

end5 = timer()
t5 = (end5 - start5) * 1000
print('方案五： ', Pi_5)
print('Running time: %s ms' % t5)

print("\n各方案时间效率字典为（这里以运行时间衡量）：")
timeEfficiency = {'方案一': t1, '方案二': t2, '方案三': t3, '方案四': t4, '方案五': t5}
print(timeEfficiency)
print('\n使用pandas 的Series数据结构进行更清晰展示：')
tdata = pd.Series(timeEfficiency)
print(tdata)

方案一：  3.1400002979112887
Running time: 0.3793000000769098 ms
方案二：  3.1390625
Running time: 0.1698999999462103 ms
方案三：  3.140000704127709
Running time: 0.1720000000204891 ms
方案四：  3.140161179474259
Running time: 0.14290000012806559 ms
方案五：  3.141592653589794
Running time: 0.11979999999311985 ms

各方案时间效率字典为（这里以运行时间衡量）：
{'方案一': 0.3793000000769098, '方案二': 0.1698999999462103, '方案三': 0.1720000000204891, '方案四': 0.14290000012806559, '方案五': 0.11979999999311985}

使用pandas 的Series数据结构进行更清晰展示：
方案一    0.3793
方案二    0.1699
方案三    0.1720
方案四    0.1429
方案五    0.1198
dtype: float64