kaggle Titanic问题(集成学习)

Titanic 生存率预测

一、问题描述

泰坦尼克号（Titanic）问题的背景就是那个大家都熟悉的『Jack and Rose』的故事，豪华游艇倒了，大家都惊恐逃生，可是救生艇的数量有限，无法人人都有，副船长发话了『lady and kid first！』，所以是否获救其实并非随机，而是基于一些背景而有rank先后的。训练和测试数据是一些乘客的个人信息以及存活状况，要尝试根据它生成合适的模型并预测其他人（test.data中的新数据）的存活状况，模型最终结果保存在predictedData.csv中。

显然，这是一个二分类问题，我们学习使用集成学习方法进行建模求解。
数据集下载地址：kaggle官网 https://www.kaggle.com/competitions/titanic/data

开始加油！

(ง •̀_•́)ง (*•̀ㅂ•́)و

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#数据处理
import numpy as np
import pandas as pd
#import os
#绘图
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# matplotlib支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

#各种模型、数据处理方法
from sklearn.preprocessing import LabelEncoder # 对数据进行编码
from sklearn.model_selection import train_test_split 
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC #支持向量机用于分类
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron #感知机
from sklearn.linear_model import SGDClassifier #随机梯度下降分类
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import GradientBoostingClassifier
from xgboost import XGBClassifier 
from lightgbm import LGBMClassifier
from sklearn.model_selection import GridSearchCV, cross_val_score, StratifiedKFold, learning_curve
from sklearn.metrics import precision_score # 精度是比率tp /（tp + fp）

import warnings
warnings.filterwarnings('ignore')

二、数据读取和查看

首先读入数据，并且初步查看数据的记录数，字段数据类型，缺失等信息。

1
2
3
4
5
# 读入数据
train_df = pd.read_csv('data/train.csv')
test_df = pd.read_csv('data/test.csv')
combine_df = pd.concat([train_df, test_df])
# concat默认拼接方式是上下堆叠
1
2
# 查看数据，展示前5行
train_df.head()

PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
0 1 0 3 Braund, Mr. Owen Harris male 22.0 1 0 A/5 21171 7.2500 NaN S
1 2 1 1 Cumings, Mrs. John Bradley (Florence Briggs Th... female 38.0 1 0 PC 17599 71.2833 C85 C
2 3 1 3 Heikkinen, Miss. Laina female 26.0 0 0 STON/O2. 3101282 7.9250 NaN S
3 4 1 1 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35.0 1 0 113803 53.1000 C123 S
4 5 0 3 Allen, Mr. William Henry male 35.0 0 0 373450 8.0500 NaN S 
1
2
# 查看数据类型等信息
train_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   PassengerId  891 non-null    int64  
 1   Survived     891 non-null    int64  
 2   Pclass       891 non-null    int64  
 3   Name         891 non-null    object 
 4   Sex          891 non-null    object 
 5   Age          714 non-null    float64
 6   SibSp        891 non-null    int64  
 7   Parch        891 non-null    int64  
 8   Ticket       891 non-null    object 
 9   Fare         891 non-null    float64
 10  Cabin        204 non-null    object 
 11  Embarked     889 non-null    object 
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB

我们可以看到部分数据存在缺失，数据类型多样，后续需要进行相关的数据处理。

1
train_df.describe()

PassengerId Survived Pclass Age SibSp Parch Fare
count 891.000000 891.000000 891.000000 714.000000 891.000000 891.000000 891.000000
mean 446.000000 0.383838 2.308642 29.699118 0.523008 0.381594 32.204208
std 257.353842 0.486592 0.836071 14.526497 1.102743 0.806057 49.693429
min 1.000000 0.000000 1.000000 0.420000 0.000000 0.000000 0.000000
25% 223.500000 0.000000 2.000000 20.125000 0.000000 0.000000 7.910400
50% 446.000000 0.000000 3.000000 28.000000 0.000000 0.000000 14.454200
75% 668.500000 1.000000 3.000000 38.000000 1.000000 0.000000 31.000000
max 891.000000 1.000000 3.000000 80.000000 8.000000 6.000000 512.329200

以上包含数值型数据（Numerical data）的统计特征

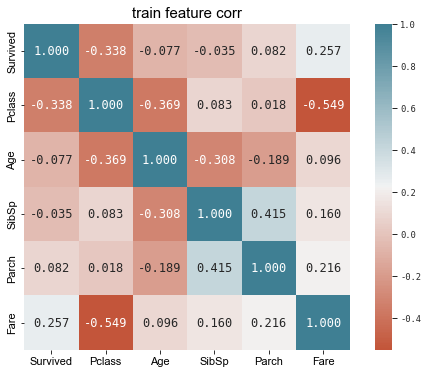
三、数据探索与变量分析

首先通过pandas的corr()函数计算相关系数矩阵，初步探索各个字段与预测变量“Survived”的关系以及各个变量之间的关系。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 通过相关系数矩阵初步观察特征与“Survived"的关系

train_df_corr = train_df.drop('PassengerId',axis=1).corr()

f, ax = plt.subplots(figsize=(9,6))
plt.style.use('ggplot')
sns.set_style('darkgrid')
sns.set(context="paper", font="monospace")

hm = sns.heatmap(train_df_corr, cmap=sns.diverging_palette(20, 220, n=200),cbar=True, annot=True, square=True, fmt='.3f',
                 annot_kws={'size':12})# 使用了seaborn的diverging_palette调色
ax.set_xticklabels(train_df_corr.index, size=11)
ax.set_yticklabels(train_df_corr.columns[:], size=11)
ax.set_title('train feature corr', fontsize=15)
Text(0.5, 1.0, 'train feature corr')


​

根据相关系数矩阵，我们初步分析可知：

  1. Fare（乘客费用）、Parch（同行的家长和孩子数目）与“Survived”正相关。
    数据显示高费用顾客更可能获救；
  2. SibSp（同行的兄弟姐妹和配偶数目）、Age（年龄）、Pclass（用户阶级）与
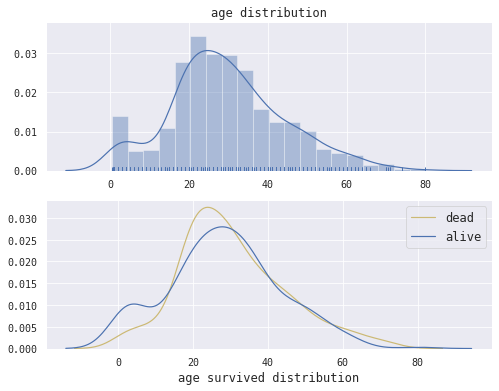
    “Survived”负相关；其中Pclass的值越小用户所属的等级越高，表示等级高的乘客更可能获救，这是具有一定的合理性的。
    ……

四、特征探索

4.1 年龄（Name）

我们将可视化展示训练数据集中年龄的整体分布以及dead和alive乘客的数量分布统计。并进行对比分析。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from scipy import stats
fig, axes = plt.subplots(2,1,figsize=(8,6))
sns.distplot(train_df.Age.dropna(), rug=True, color='b', ax=axes[0])
ax0 = axes[0]
ax0.tick_params(labelsize=10)
ax0.set_title('age distribution',fontsize=12)
ax0.set_xlabel('')
ax0.set_ylabel('')

ax1 = axes[1]
# ax1.set_title('age survived distribution')
k1 = sns.distplot(train_df[train_df.Survived==0].Age.dropna(), hist=False, color='y', ax=ax1, label='dead')
k2 = sns.distplot(train_df[train_df.Survived==1].Age.dropna(), hist=False, color='b', ax=ax1, label='alive')
ax1.tick_params(labelsize=10)
ax1.set_xlabel('age survived distribution',fontsize=12)
ax1.set_ylabel('')

ax1.legend(fontsize=12)
<matplotlib.legend.Legend at 0x24b9bfaffd0>

乘客的年龄集中在20-40岁，所以主要为青年人和中年人。从age survived distribution表中我们可以发现，小孩获救似乎更容易一些，这个结果也有一定的社会基础，灾难时刻，大多数人可能选择站出来保护妇女和儿童。

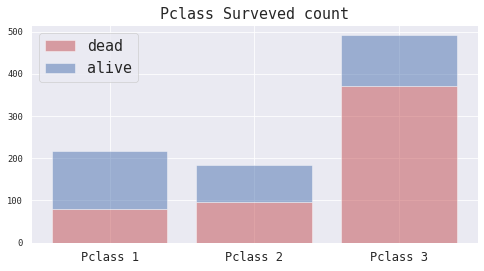
4.2 用户阶级（Pclass）

我们绘制柱形图展示不同Pclass（1， 2 ， 3）的乘客获救与未获救的数量，以对比发现Pclass与“Survived”的关系。

1
2
3
4
5
6
7
8
9
10
11
y_dead = train_df[train_df.Survived==0].groupby('Pclass')['Survived'].count()
y_alive = train_df[train_df.Survived==1].groupby('Pclass')['Survived'].count()

pos = [1,2,3]
ax = plt.figure(figsize=(8,4)).add_subplot(1,1,1)
ax.bar(pos, y_dead, color='r', alpha=0.5, label='dead')
ax.bar(pos, y_alive, color='b', bottom=y_dead, alpha=0.5, label='alive')
ax.legend(fontsize=15, loc='best')
ax.set_xticks(pos)
ax.set_xticklabels(['Pclass %d'%(i) for i in range(1,4)], size=12)
ax.set_title('Pclass Surveved count', size=15)
Text(0.5, 1.0, 'Pclass Surveved count')

Pclass从1至3等级递减，即1可以理解为头等乘客。我们发现在Pclass=1的记录中，乘客的获救比例明显最高，这是一个有趣的现象。或许更高等的乘客配备了更好的保护措施。

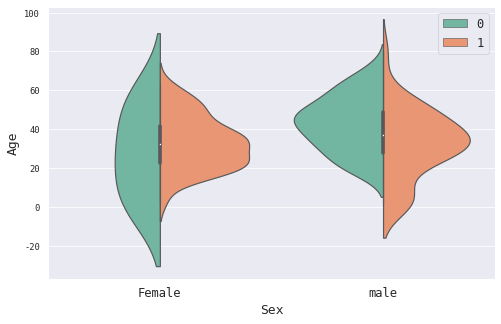
4.3 性别（Sex）

1
2
3
4
5
# 统计性别和获救的数量

print(train_df.Sex.value_counts())
print('-------------------------------')
print(train_df.groupby('Sex')['Survived'].mean())
male      577
female    314
Name: Sex, dtype: int64
-------------------------------
Sex
female    0.742038
male      0.188908
Name: Survived, dtype: float64

我们注意到，男性的数量偏多，同时数据展现出来的女性的存活率（0.742038）远远高于男性（0.188908）
这符合我们在年龄（Name）中的有关猜想。我们在后续的特征处理中应该注意这一特点。

1
2
3
4
5
6
7
8
# violinplot(小提琴图)可视化展示

ax = plt.figure(figsize=(8,5)).add_subplot(1,1,1)
sns.violinplot(x='Sex', y='Age', hue='Survived', palette="Set2", data=train_df.dropna(), split=True)
ax.set_xlabel('Sex', size=13)
ax.set_xticklabels(['Female', 'male'], size=12)
ax.set_ylabel('Age', size=13)
ax.legend(fontsize=12,loc='best')
<matplotlib.legend.Legend at 0x24b9e256f40>

图例中0表示’Survived’=0，即未获救；图表具有多个维度，可以反映不同性别以及是否获救的乘客的大致分布情况。
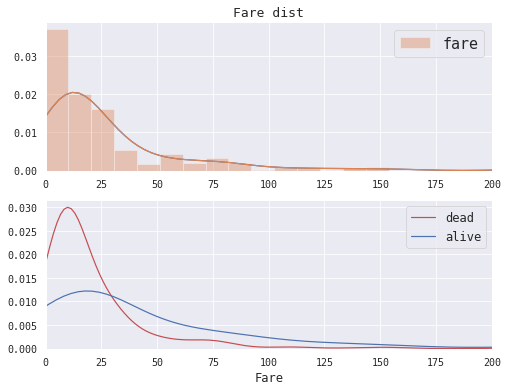
分析结果显示，无论男女中青年容易获救；相比于女性，男性老年和小孩的获救比例更大。

4.4 Frae(票价)

我们分别绘制票价的总体分布图和dead和alive类型的票价分布对比图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 票价的总体分布图
fig = plt.figure(figsize=(8, 6))
ax = plt.subplot2grid((2,2), (0,0), colspan=2)

ax.tick_params(labelsize=10)
ax.set_title('Fare dist', size=13)
sns.kdeplot(train_df.Fare, ax=ax)
sns.distplot(train_df.Fare,label='fare', ax=ax)
ax.legend(fontsize=15)
pos = range(0,201,25)
ax.set_xticks(pos)
ax.set_xlim([0, 200])
ax.set_xlabel('')
ax.set_ylabel('')

# dead和alive分别统计的票价分布曲线对比图
ax1 = plt.subplot2grid((2,2), (1,0), colspan=2)
ax1.tick_params(labelsize=10)
sns.distplot(train_df[train_df.Survived==0].Fare, ax=ax1,hist=False, label='dead', color='r')
sns.distplot(train_df[train_df.Survived==1].Fare, ax=ax1,hist=False, label='alive',  color='b')
ax1.set_xlim([0,200])
ax1.legend(fontsize=12)

ax1.set_xlabel('Fare', size=12)
ax1.set_ylabel('')
Text(0, 0.5, '')

图中可以看到，低票价（Fare）的乘客中死亡比例极高，而高票价的乘客中获救的人似乎要更多。
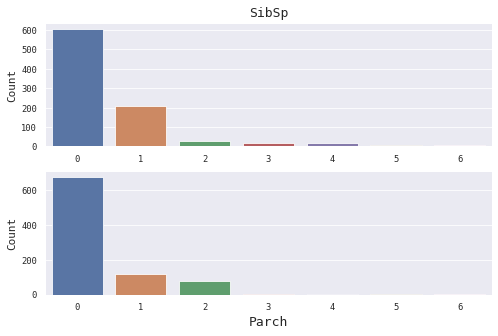
同时我们注意到，Fare的分布太宽，后续数据处理可以做一下scaling，加速模型收敛。

4.5 表亲和直亲(SibSp和Parch)

SibSp描述了泰坦尼克号上与乘客同行的兄弟姐妹（Siblings）和配偶（Spouse）数目；
而Parch描述了泰坦尼克号上与乘客同行的家长（Parents）和孩子（Children）数目。

1
2
3
4
5
6
7
8
9
10
11
12
# 首先查看数据分布特征
fig = plt.figure(figsize=(8, 5))
ax1 = fig.add_subplot(2, 1, 1)
sns.countplot(train_df.SibSp)
ax1.set_title('SibSp', size=13)
ax1.set_xlabel('')
ax1.set_ylabel('Count',size=11)

ax2 = fig.add_subplot(2, 1, 2, sharex=ax1)
sns.countplot(train_df.Parch)
ax2.set_xlabel('Parch', size=13)
ax2.set_ylabel('Count',size=11)
Text(0, 0.5, 'Count')


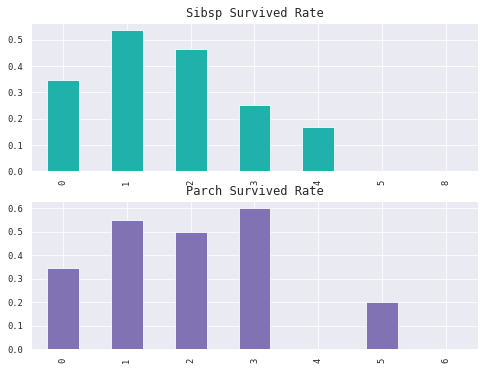
1
2
3
4
5
6
7
8
9
10
11
12
# 统计对比不同sibsp & parch情况下的获救比例

fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(2, 1, 1)
train_df.groupby('SibSp')['Survived'].mean().plot(kind='bar',ax= ax1,color='lightseagreen')
ax1.set_title('Sibsp Survived Rate', size=12)
ax1.set_xlabel('')

ax2 = fig.add_subplot(2, 1, 2)
train_df.groupby('Parch')['Survived'].mean().plot(kind='bar',ax= ax2,color='m')
ax2.set_title('Parch Survived Rate', size=12)
ax2.set_xlabel('')
Text(0.5, 0, '')

分组统计不同亲戚类型,即表亲和直亲(SibSp和Parch)和数量的获救率。我们发现，获救率与亲戚的关系可能并不具有简单的线性关系。

五、特征工程

5.1 Name特征处理

充分挖掘和提取Titanic数据集的特征可以有效提高模型精度。因此，我们对name字段进行挖掘和特征的提取

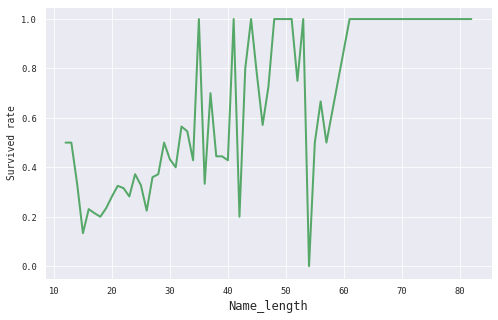
5.2 Name_Len特征

由于西方人的名字长度差别较大，且含义丰富，我们首先探索一下名字长度这个特征：

1
2
3
train_df.groupby(train_df.Name.apply(lambda x: len(x)))['Survived'].mean().plot(figsize=(8,5),linewidth=2,color='g')
plt.xlabel('Name_length',fontsize=12)
plt.ylabel('Survived rate')
Text(0, 0.5, 'Survived rate')

可以看到名字的长度和获救率还是有一定的正向关系的，可以考虑加入Name_Len特征：

1
2
3
4
5
# 加入Name_Len特征
combine_df['Name_Len'] = combine_df['Name'].apply(lambda x: len(x))

# Name_Len数据分箱
combine_df['Name_Len'] = pd.qcut(combine_df['Name_Len'],5)
注：

数据分箱（也称为离散分箱或分段）是一种数据预处理技术，用于减少次要观察误差的影响，是一种将多个连续值分组为较少数量的“分箱”的方法。

5.3 Title特征

西方人名字中含有的称谓信息(数据集中名字中间的单词)也可以在很大程度上反映一个人的身份地位，从数据中提取”Title”（称谓）也可以作为特征，由于有些称谓的人数量过少，我们还需要做一个映射（分组），将一组等效的称谓合并在一起。

几条有关英语称谓的解释：
Mme：相当于Mrs Ms：Ms.或Mz 美国近来用来称呼婚姻状态不明的妇女
Jonkheer: 乡绅 Col：中校:Lieutenant Colonel(Lt. Col.)上校:Colonel(Col.)
Lady：贵族夫人的称呼 Major：少校
Don唐：是西班牙语中贵族和有地位者的尊称 Mlle: 小姐
sir：懂的都懂 Rev：牧师
the Countess：女伯爵 测试集合中的Dona：女士尊称 
1
2
3
4
5
6
7
8
9
# 称谓的提取和合并
combine_df['Title'] = combine_df['Name'].apply(lambda x: x.split(', ')[1]).apply(lambda x: x.split('.')[0])
combine_df['Title'] = combine_df['Title'].replace(['Don','Dona', 'Major', 'Capt', 'Jonkheer', 'Rev', 'Col','Sir','Dr'],'Mr')
combine_df['Title'] = combine_df['Title'].replace(['Mlle','Ms'], 'Miss')
combine_df['Title'] = combine_df['Title'].replace(['the Countess','Mme','Lady','Dr'], 'Mrs')

# 分类变量编码，转换为哑变量处理
df = pd.get_dummies(combine_df['Title'],prefix='Title')# prefix：表示列名的前缀
combine_df = pd.concat([combine_df,df],axis=1)

在特征探索阶段，我们发现男性和女性的获救率分别为女性的0.742038和男性的0.188908；
女性死亡以及男性存活概率明显较低，为了提升模型对于这一类群体的识别能力，我们分析数据并找到了一个重要特征“Family”，同一个family下的生存死亡模式有很大程度上是相关的，例如：有一个family有一个女性死亡，这个family其他的女性的死亡概率也比较高。

1
2
3
4
5
6
7
8
9
10
#我们标注出这些特殊的family

combine_df['Surname'] = combine_df['Name'].apply(lambda x:x.split(',')[0])
dead_female_surname = list(set(combine_df[(combine_df.Sex=='female') & (combine_df.Age>=12)
                              & (combine_df.Survived==0) & ((combine_df.Parch>0) | (combine_df.SibSp > 0))]['Surname'].values))
survive_male_surname = list(set(combine_df[(combine_df.Sex=='male') & (combine_df.Age>=12)
                              & (combine_df.Survived==1) & ((combine_df.Parch>0) | (combine_df.SibSp > 0))]['Surname'].values))
combine_df['Dead_female_family'] = np.where(combine_df['Surname'].isin(dead_female_surname),0,1)
combine_df['Survive_male_family'] = np.where(combine_df['Surname'].isin(survive_male_surname),0,1)
combine_df = combine_df.drop(['Name','Surname'],axis=1)

5.4 Age特征

根据特征探索阶段的分析，小孩的获救率明显较高，可以添加一个小孩标签属性（IsChild）：

1
2
3
4
5
6
7
#Age & isChild
group = combine_df.groupby(['Title', 'Pclass'])['Age']
combine_df['Age'] = group.transform(lambda x: x.fillna(x.median()))
combine_df = combine_df.drop('Title',axis=1)
combine_df['IsChild'] = np.where(combine_df['Age']<=12,1,0)
combine_df['Age'] = pd.cut(combine_df['Age'],5)
combine_df = combine_df.drop('Age',axis=1)

5.5 Familysize

将上面提取过的Familysize再离散化

1
2
3
4
5
6
# 分箱，将Familysize=0标注为'solo',Familysize>3为'big'，中间为'normal'，然后对分类变量编码，转换为哑变量处理

combine_df['FamilySize'] = np.where(combine_df['SibSp']+combine_df['Parch']==0, 'Alone',
                                    np.where(combine_df['SibSp']+combine_df['Parch']<=3, 'Small', 'Big'))
df = pd.get_dummies(combine_df['FamilySize'],prefix='FamilySize')
combine_df = pd.concat([combine_df,df],axis=1).drop(['SibSp','Parch','FamilySize'],axis=1)

5.6 Ticket特征

统计发现，【’1’, ‘2’, ‘P’】开头的Ticket获救率更高。可以标注为’High_Survival_Ticket’型票；同理【’A’,’W’,’3’,’7’】为’Low_Survival_Ticket’型票。这样得到High_Survival_Ticket和Low_Survival_Ticket两个新的特征。

1
2
3
4
5
6
combine_df['Ticket_Lett'] = combine_df['Ticket'].apply(lambda x: str(x)[0])
combine_df['Ticket_Lett'] = combine_df['Ticket_Lett'].apply(lambda x: str(x))

combine_df['High_Survival_Ticket'] = np.where(combine_df['Ticket_Lett'].isin(['1', '2', 'P']),1,0)
combine_df['Low_Survival_Ticket'] = np.where(combine_df['Ticket_Lett'].isin(['A','W','3','7']),1,0)
combine_df = combine_df.drop(['Ticket','Ticket_Lett'],axis=1)

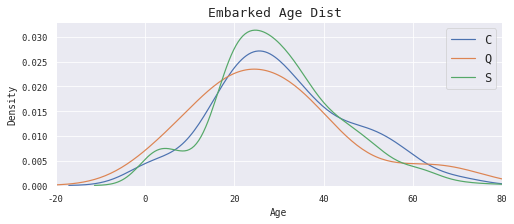
5.7 Embarked特征

1
2
3
4
5
6
7
ax = plt.figure(figsize=(8,3)).add_subplot(111)
ax.set_xlim([-20, 80])
sns.kdeplot(train_df[train_df.Embarked=='C'].Age.dropna(), ax=ax, label='C')
sns.kdeplot(train_df[train_df.Embarked=='Q'].Age.dropna(), ax=ax, label='Q')
sns.kdeplot(train_df[train_df.Embarked=='S'].Age.dropna(), ax=ax, label='S')
ax.legend(fontsize=12)
ax.set_title('Embarked Age Dist ', size=13)
Text(0.5, 1.0, 'Embarked Age Dist ')

Embarked字段只有个别缺失，我们选择数量最多且年龄分布正常的港口进行填充

1
2
3
4
5
# 缺失港口信息填充S，并转换为哑变量

combine_df.Embarked = combine_df.Embarked.fillna('S')
df = pd.get_dummies(combine_df['Embarked'],prefix='Embarked')
combine_df = pd.concat([combine_df,df],axis=1).drop('Embarked',axis=1)

5.8 Cabin特征

Cabin特征大量缺失，我们将其转化为Cabin_isNull特征，取值域为0和1

1
2
combine_df['Cabin_isNull'] = np.where(combine_df['Cabin'].isnull(),0,1)
combine_df = combine_df.drop('Cabin',axis=1)

5.9 Pclass & Sex特征

Pclass & Sex特征进行分类数据编码，转化为哑变量：

1
2
3
4
5
6
7
# Pclass
df = pd.get_dummies(combine_df['Pclass'],prefix='Pclass')
combine_df = pd.concat([combine_df,df],axis=1).drop('Pclass',axis=1)

# Sex
df = pd.get_dummies(combine_df['Sex'],prefix='Sex')
combine_df = pd.concat([combine_df,df],axis=1).drop('Sex',axis=1)

5.10 Fare特征

缺省值用众数填充，之后进行离散化

1
2
3
4
5
#Fare
combine_df['Fare'].fillna(combine_df['Fare'].dropna().median(),inplace=True)
combine_df['Low_Fare'] = np.where(combine_df['Fare']<=8.662,1,0)
combine_df['High_Fare'] = np.where(combine_df['Fare']>=26,1,0)
combine_df = combine_df.drop('Fare',axis=1)

六、 模型训练/测试

查看我们现在有哪些特征：

1
combine_df.columns
Index(['PassengerId', 'Survived', 'Name_Len', 'Title_Master', 'Title_Miss',
       'Title_Mr', 'Title_Mrs', 'Dead_female_family', 'Survive_male_family',
       'IsChild', 'FamilySize_Alone', 'FamilySize_Big', 'FamilySize_Small',
       'High_Survival_Ticket', 'Low_Survival_Ticket', 'Embarked_C',
       'Embarked_Q', 'Embarked_S', 'Cabin_isNull', 'Pclass_1', 'Pclass_2',
       'Pclass_3', 'Sex_female', 'Sex_male', 'Low_Fare', 'High_Fare'],
      dtype='object')

所有特征转化成数值型编码：

LabelEncoder是用来对分类型特征值进行编码，即对不连续的数值或文本进行编码。其中包含以下常用方法：

  1. fit(y) ：fit可看做一本空字典，y可看作要塞到字典中的词。
  2. fit_transform(y)：相当于先进行fit再进行transform，即把y塞到字典中去以后再进行transform得到索引值。
  3. inverse_transform(y)：根据索引值y获得原始数据。
  4. transform(y) ：将y转变成索引值。
1
2
3
4
5
6
7
8
features = combine_df.drop(["PassengerId","Survived"], axis=1).columns
le = LabelEncoder()
for feature in features:
    combine_df[feature]=le.fit_transform(combine_df[feature])
    # 和以下两行等价
    # le = le.fit(combine_df[feature])# fit(),将所有特征转化成数值型编码
    # combine_df[feature] = le.transform(combine_df[feature])
combine_df

PassengerId Survived Name_Len Title_Master Title_Miss Title_Mr Title_Mrs Dead_female_family Survive_male_family IsChild ... Embarked_Q Embarked_S Cabin_isNull Pclass_1 Pclass_2 Pclass_3 Sex_female Sex_male Low_Fare High_Fare
0 1 0.0 1 0 0 1 0 1 1 0 ... 0 1 0 0 0 1 0 1 1 0
1 2 1.0 4 0 0 0 1 1 1 0 ... 0 0 1 1 0 0 1 0 0 1
2 3 1.0 1 0 1 0 0 1 1 0 ... 0 1 0 0 0 1 1 0 1 0
3 4 1.0 4 0 0 0 1 1 1 0 ... 0 1 1 1 0 0 1 0 0 1
4 5 0.0 2 0 0 1 0 1 1 0 ... 0 1 0 0 0 1 0 1 1 0
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
413 1305 NaN 0 0 0 1 0 1 1 0 ... 0 1 0 0 0 1 0 1 1 0
414 1306 NaN 3 0 0 1 0 1 1 0 ... 0 0 1 1 0 0 1 0 0 1
415 1307 NaN 3 0 0 1 0 1 1 0 ... 0 1 0 0 0 1 0 1 1 0
416 1308 NaN 0 0 0 1 0 1 1 0 ... 0 1 0 0 0 1 0 1 1 0
417 1309 NaN 2 1 0 0 0 1 1 1 ... 0 0 0 0 0 1 0 1 0 0

1309 rows × 26 columns

6.1 模型搭建

1
2
3
X_all = combine_df.iloc[:891,:].drop(["PassengerId","Survived"], axis=1)
Y_all = combine_df.iloc[:891,:]["Survived"]
X_test = combine_df.iloc[891:,:].drop(["PassengerId","Survived"], axis=1)

6.2 模型与参数初始化

1
2
3
4
5
6
7
8
9
10
11
# 考察逻辑回归、支持向量机、最近邻、决策树、随机森林、gbdt、xgbGBDT几类算法的性能
logreg = LogisticRegression()
svc = SVC()
knn = KNeighborsClassifier(n_neighbors = 5)
decision_tree = DecisionTreeClassifier()
random_forest = RandomForestClassifier(n_estimators=300,min_samples_leaf=4,class_weight={0:0.745,1:0.255})
gbdt = GradientBoostingClassifier(n_estimators=300,learning_rate=0.05,max_depth=3)
xgb = XGBClassifier(max_depth=6, n_estimators=400, learning_rate=0.02)
lgb = LGBMClassifier(max_depth=6, n_estimators=300, learning_rate=0.02)
clfs = [logreg, svc, knn, decision_tree, random_forest, gbdt, xgb, lgb]

6.3 网格参数搜索

sklearn.model_selection库中有GridSearchCV方法，作用是搜索模型的最优参数。
我们使用GridSearchCV初步选择参数，后续再不断返回调参。

1
2
3
4
5
6
7
8
9
10
11
12
# clfs = [logreg, svc, knn, decision_tree, random_forest, gbdt, xgb, lgb]

#XGboost 参数搜索
gsCv = GridSearchCV(xgb,
                   {'max_depth': [5,6,7,8],
                    'n_estimators': [300,400,500],
                   'learning_rate':[0.01,0.02,0.03,0.04]
                   })
gsCv.fit(X_all,Y_all)

print(gsCv.best_score_)
print(gsCv.best_params_)
0.8911116690728769
{'learning_rate': 0.02, 'max_depth': 6, 'n_estimators': 400}

1
2
3
4
5
6
7
8
9
10
#lightgbm 参数搜索
gsCv = GridSearchCV(lgb,
                   {'max_depth': [5,6,7,8],
                    'n_estimators': [200,300,400,500],
                   'learning_rate':[0.01,0.02,0.03,0.04]
                   })
gsCv.fit(X_all,Y_all)

print(gsCv.best_score_)
print(gsCv.best_params_)
0.8866172870504048
{'learning_rate': 0.02, 'max_depth': 6, 'n_estimators': 300}

1
2
3
4
5
6
7
8
9
10
#GBDT 参数搜索
gsCv = GridSearchCV(gbdt,
                   {'max_depth': [2,3,4,5,6],
                    'n_estimators': [200,300,400,500],
                   'learning_rate':[0.04,0.05,0.06]
                   })
gsCv.fit(X_all,Y_all)

print(gsCv.best_score_)
print(gsCv.best_params_)
0.8899943506371226
{'learning_rate': 0.05, 'max_depth': 3, 'n_estimators': 300}

1
2
3
4
5
6
7
#KNN 参数搜索
gsCv = GridSearchCV(knn,
                   {'n_neighbors':[3,4,5,6,7]})
gsCv.fit(X_all,Y_all)

print(gsCv.best_score_)
print(gsCv.best_params_)
0.8529659155106396
{'n_neighbors': 5}

6.4 K折交叉验证

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# K折交叉验证

kfold = 10
cv_results = []
for classifier in clfs :
    cv_results.append(cross_val_score(classifier, X_all.values, y = Y_all.values, scoring = "accuracy", cv = kfold, n_jobs=4))

# cv_results 为8*10的结果矩阵
cv_means = []
cv_std = []
for cv_result in cv_results:
    cv_means.append(cv_result.mean())
    cv_std.append(cv_result.std())

ag = ["logreg","SVC",'KNN','decision_tree',"random_forest","GBDT","xgbGBDT", "LGB"]
cv_res = pd.DataFrame({"CrossValMeans":cv_means,"CrossValerrors": cv_std,
                       "Algorithm":ag})

g = sns.barplot("CrossValMeans","Algorithm",data = cv_res, palette="Blues")
g.set_xlabel("CrossValMeans",fontsize=10)
g.set_ylabel('')
plt.xticks(rotation=30)
g = g.set_title("10-fold Cross validation scores",fontsize=12)

1
2
3
# 展示10-fold Cross validation的均值得分结果
for i in range(8):
    print("{} : {}".format(ag[i],cv_means[i]))
logreg : 0.8731585518102373
SVC : 0.8776404494382023
KNN : 0.8540823970037452
decision_tree : 0.8652559300873908
random_forest : 0.8563920099875156
GBDT : 0.8832459425717852
xgbGBDT : 0.8843820224719101
LGB : 0.8799001248439451

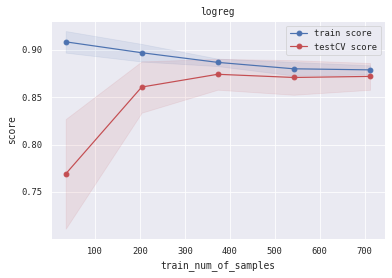
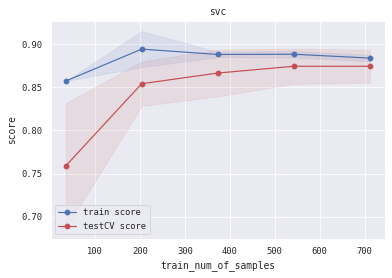
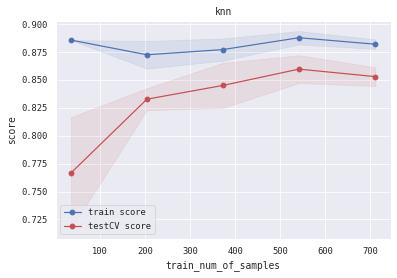
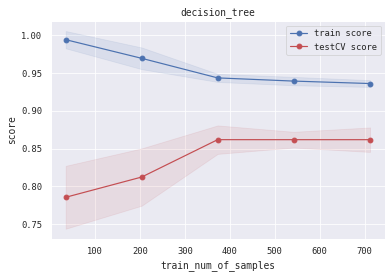
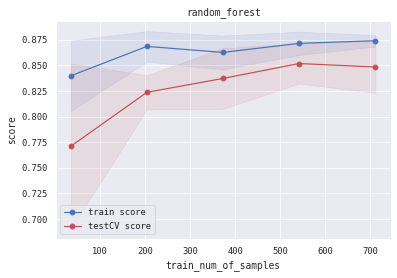
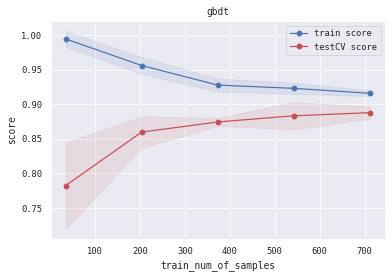
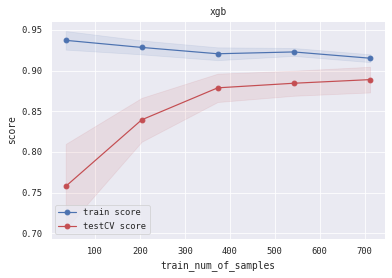
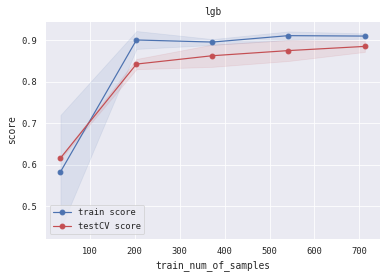
6.5 训练/验证过程可视化

将模型训练过程的学习曲线打印出来，看下是否存在过拟合/欠拟合情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 用sklearn的learning_curve得到training_score和cv_score，使用matplotlib画出learning curve

def plot_learning_curve(clf, title, X, y, ylim=None, cv=None, n_jobs=3, train_sizes=np.linspace(.05, 1., 5)):
    train_sizes, train_scores, test_scores = learning_curve(
        clf, X, y, train_sizes=train_sizes)
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    
    ax = plt.figure().add_subplot(111)
    ax.set_title(title)
    if ylim is not None:
        ax.ylim(*ylim)
    ax.set_xlabel(u"train_num_of_samples")
    ax.set_ylabel(u"score")

    ax.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, 
                     alpha=0.1, color="b")
    ax.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, 
                     alpha=0.1, color="r")
    ax.plot(train_sizes, train_scores_mean, 'o-', color="b", label=u"train score")
    ax.plot(train_sizes, test_scores_mean, 'o-', color="r", label=u"testCV score")

    ax.legend(loc="best")

    midpoint = ((train_scores_mean[-1] + train_scores_std[-1]) + (test_scores_mean[-1] - test_scores_std[-1])) / 2
    diff = (train_scores_mean[-1] + train_scores_std[-1]) - (test_scores_mean[-1] - test_scores_std[-1])
    return midpoint, diff

alg_list=['logreg', 'svc', 'knn', 'decision_tree', 'random_forest', 'gbdt', 'xgb', 'lgb']

plot_learning_curve(clfs[0], alg_list[0], X_all, Y_all)
plot_learning_curve(clfs[1], alg_list[1], X_all, Y_all)
plot_learning_curve(clfs[2], alg_list[2], X_all, Y_all)
plot_learning_curve(clfs[3], alg_list[3], X_all, Y_all)
plot_learning_curve(clfs[4], alg_list[4], X_all, Y_all)
plot_learning_curve(clfs[5], alg_list[5], X_all, Y_all)
plot_learning_curve(clfs[6], alg_list[6], X_all, Y_all)
plot_learning_curve(clfs[7], alg_list[7], X_all, Y_all)
(0.8944812361959231, 0.04456088047192275)


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from sklearn.metrics import precision_score

# 定义集成框架
class Bagging(object):
    # sklearn机器学习算法的实现都属于estimators的子类：
    def __init__(self,estimators):
        self.estimator_names = []
        self.estimators = []
        for i in estimators:
            self.estimator_names.append(i[0])
            self.estimators.append(i[1])
        self.clf = LogisticRegression()
    
    def fit(self, train_x, train_y):
        for i in self.estimators:
            i.fit(train_x,train_y)
        x = np.array([i.predict(train_x) for i in self.estimators]).T
        y = train_y
        self.clf.fit(x, y)
    
    def predict(self,x):
        x = np.array([i.predict(x) for i in self.estimators]).T
        #print(x)
        return self.clf.predict(x)
        
    
    def score(self,x,y):
        s = precision_score(y,self.predict(x))
        #print(s)
        return s

6.6 模型集成与验证（Bagging）

选择训练结果最好的四个基学习器进行集成（Bagging）

1
2
3
4
5
6
7
8
9
10
# logreg = LogisticRegression()
# random_forest = RandomForestClassifier(n_estimators=300,min_samples_leaf=4,class_weight={0:0.745,1:0.255})
# gbdt = GradientBoostingClassifier(n_estimators=500,learning_rate=0.03,max_depth=3)
#xgb = XGBClassifier(max_depth=3, n_estimators=500, learning_rate=0.03)
#clfs = [logreg, svc, knn, decision_tree, random_forest, gbdt, xgb]

# 选择训练结果最好的四个基学习器集成（Bagging）

bag = Bagging([('xgb',xgb),('logreg',logreg),('gbdt',gbdt), ("lgb", lgb)])
from sklearn.metrics import precision_score

X_all，Y_all中按照4：1的比例划分训练数据和测试数据，简化起见没有划分验证集（validation data）用于参数调优，使用训练数据训练我们的集成模型。在划分的测试集上进行预测，并计算模型准确率（Accuracy）。

1
2
3
4
5
6
7
8
9
score = 0
for i in range(0,20):
    num_test = 0.20
    X_train, X_cv, Y_train, Y_cv = train_test_split(X_all.values, Y_all.values, test_size=num_test)
    bag.fit(X_train, Y_train)
    #Y_test = bag.predict(X_test)
    acc_ = round(bag.score(X_cv, Y_cv) * 100, 2)
    score+=acc_
score/20
88.43750000000001

七、进行预测

1
2
3
4
5
6
7
8
# submission存储了预测结果
bag.fit(X_all.values, Y_all.values)
Y_test = bag.predict(X_test.values).astype(int)
submission = pd.DataFrame({
        "PassengerId": test_df["PassengerId"],
        "Survived": Y_test
    })
submission.to_csv(r'predictedData.csv', index=False)

八、评价与总结

  • 数据集选择了经典的kaggle数据竞赛中的Titanic数据集。对于我这样的数据科学、机器学习初学者来说，在该数据集基础上可以找到大量来自大神的实现参考，利于快速上手入门；
  • 没有花时间在’’炼丹’’上，只是使用sklearn.model_selection模块中的网格参数搜索函数GridSearchCV进行了较为简单的参数选择。不过我们还是在训练集和测试集都表现出了较高的精度 ，同时没有明显的过拟合或者欠拟合现象。
  • 起初只是想学习并做一个使用GBDT算法的小项目（基于XGboost），但是发现了大神使用集成的方法进行过相关的实现，所以虚心进行了学习 (•ิ_•ิ)
  • 本人知识，经验十分有限，如果有处理不当或者错误的地方还请谅解。

完结撒花

｡:.ﾟヽ(｡◕‿◕｡)ﾉﾟ.:｡+ﾟ

Machine Learning > Kaggle > 集成学习
#集成学习 #Titanic #Kaggle #ML
kaggle Titanic问题(集成学习)
https://e-alan.github.io/2022/11/03/kaggle Titanic问题(集成学习)/
作者
Yubiao Wang
发布于
2022年11月3日
许可协议